Steam Distribution

Pipes and Pipe Sizing for steam distribution
Pipe sizing is a crucial aspect of steam system design. This tutorial offers detailed advice on standards, schedules, materials and sizing for various saturated and superheated steam duties.
Contents
What are the international piping standards?
There are a number of piping standards in existence around the world, but arguably the most global are those derived by the American Petroleum Institute (API), where pipes are categorised in schedule numbers.
These schedule numbers bear a relation to the pressure rating of the piping. There are eleven Schedules ranging from the lowest at 5 through 10, 20, 30, 40, 60, 80, 100, 120, 140 to schedule No. 160. For nominal size piping 150 mm and smaller, Schedule 40 (sometimes called ‘standard weight’) is the lightest that would be specified for steam applications.
Regardless of schedule number, pipes of a particular size all have the same outside diameter (not withstanding manufacturing tolerances). As the schedule number increases, the wall thickness increases, and the actual bore is reduced. For example:
- A 100 mm Schedule 40 pipe has an outside diameter of 114.30 mm, a wall thickness of 6.02 mm, giving a bore of 102.26 mm.
- A 100 mm Schedule 80 pipe has an outside diameter of 114.30 mm, a wall thickness of 8.56 mm, giving a bore of 97.18 mm.
Only Schedules 40 and 80 cover the full range from 15 mm up to 600 mm nominal sizes and are the most commonly used schedule for steam pipe installations.
This Module considers Schedule 40 pipework as covered in BS 1600.
Tables of schedule numbers can be obtained from BS 1600 which are used as a reference for the nominal pipe size and wall thickness in millimetres. Table 10.2.1 compares the actual bore sizes of different sized pipes, for different schedule numbers.
In mainland Europe, pipe is manufactured to DIN standards, and DIN 2448 pipe is included in Table 10.2.1.
Table 10.2.1 Comparison of pipe standards and actual bore diameters.
| Nominal size pip (mm) | 15 | 20 | 25 | 32 | 40 | 50 | 65 | 80 | 100 | 150 | |
| Bore (mm) | Schedule 40 | 15.8 | 21.0 | 26.6 | 35.1 | 40.9 | 52.5 | 62.7 | 77.9 | 102.3 | 154.1 |
| Schedule 80 | 13.8 | 18.9 | 24.3 | 32.5 | 38.1 | 49.2 | 59.0 | 73.7 | 97.2 | 146.4 | |
| Schedule 160 | 11.7 | 15.6 | 20.7 | 29.5 | 34.0 | 42.8 | 53.9 | 66.6 | 87.3 | 131.8 | |
| DIN 2448 | 17.3 | 22.3 | 28.5 | 37.2 | 43.1 | 60.3 | 70.3 | 82.5 | 107.1 | 159.3 | |
In the United Kingdom, piping to EN 10255, (steel tubes and tubulars suitable for screwing to BS 21 threads) is also used in applications where the pipe is screwed rather than flanged. They are commonly referred to as ‘Blue Band’ and ‘Red Band’; this being due to their banded identification marks. The different colours refer to particular grades of pipe:
- Red Band, being heavy grade, is commonly used for steam pipe applications.
- Blue Band, being medium grade, is commonly used for air distribution systems, although it is sometimes used for low-pressure steam systems.
The coloured bands are 50 mm wide, and their positions on the pipe denote its length. Pipes less than 4 metres in length only have a coloured band at one end, while pipes of 4 to 7 metres in length have a coloured band at either end.


What is the typical pipe material for steam systems?
Pipes for steam systems are commonly manufactured from carbon steel to ASME B 16.9 A106. The same material may be used for condensate lines, although copper tubing is preferred in some industries.
For high temperature superheated steam mains, additional alloying elements, such as chromium and molybdenum, are included to improve tensile strength and creep resistance at high temperatures.
Typically, pipes are supplied in 6 metre lengths.
Pipeline sizing
The importance of pipeline sizing
The objective of any fluid distribution system is to supply the fluid at the correct pressure to the point of use. It follows, therefore, that pressure drop through the distribution system is an important feature.
Pipeline sizing for Liquids
Bernoulli’s Theorem (Daniel Bernoulli 1700 - 1782) is discussed in Block 4 - Flowmetering. D’Arcy (D’Arcy Thompson 1860 - 1948) added that for fluid flow to occur, there must be more energy at Point 1 than Point 2 (see Figure 10.2.3). The difference in energy is used to overcome frictional resistance between the pipe and the flowing fluid.
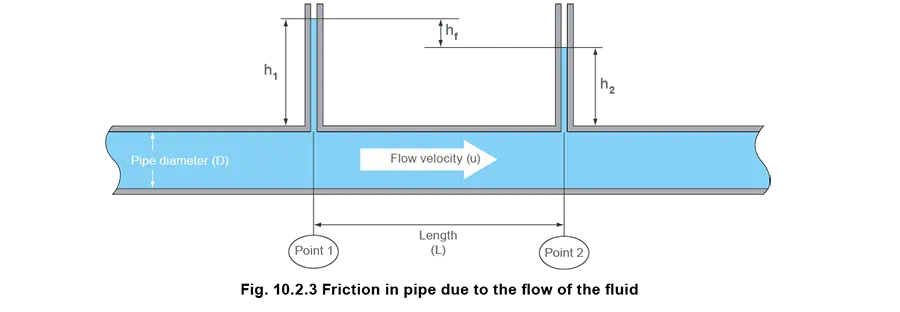
Bernoulli relates changes in the total energy of a flowing fluid to energy dissipation expressed either in terms of a head loss hf (m) or specific energy loss g hf (J/kg). This, in itself, is not very useful without being able to predict the pressure losses that will occur in particular circumstances.
Here, one of the most important mechanisms of energy dissipation within a flowing fluid is introduced, that is, the loss in total mechanical energy due to friction at the wall of a uniform pipe carrying a steady flow of fluid.
The loss in the total energy of fluid flowing through a circular pipe must depend on:
L = The length of the pipe (m)
D = The pipe diameter (m)
u = The mean velocity of the fluid flow (m/s)
μ = The dynamic viscosity of the fluid (kg/m s = Pa s)
italic-p - body text.jpg= The fluid density (kg/m³)
kS = The roughness of the pipe wall* (m)
* Since the energy dissipation is associated with shear stress at the pipe wall, the nature of the wall surface will be influential, as a smooth surface will interact with the fluid in a different way than a rough surface.
All these variables are brought together in the D’Arcy-Weisbach equation (often referred to as the D’Arcy equation), and shown as Equation 10.2.1. This equation also introduces a dimensionless term referred to as the friction factor, which relates the absolute pipe roughness to the density, velocity and viscosity of the fluid and the pipe diameter.
The term that relates fluid density, velocity and viscosity and the pipe diameter is called the Reynolds number, named after Osborne Reynolds (1842-1912, of Owens College, Manchester, United Kingdom), who pioneered this technical approach to energy losses in flowing fluids circa 1883.
The D’Arcy equation (Equation 10.2.1):
Readers in some parts of the world may recognise the D’Arcy equation in a slightly different form, as shown in Equation 10.2.2. Equation 10.2.2 is similar to Equation 10.2.1 but does not contain the constant 4.


The reason for the difference is the type of friction factor used. It is essential that the right version of the D’Arcy equation be used with the selected friction factor. Matching the wrong equation to the wrong friction factor will result in a 400% error and it is therefore important that the correct combination of equation and friction factor is utilised. Many textbooks simply do not indicate which friction factors are defined, and a judgement must sometimes be based on the magnitudes quoted.
Equation 10.2.2 tends to be used by those who traditionally work in Imperial units, and still tends to be used by practitioners in the United States and Pacific rim regions even when metric pipe sizes are quoted. Equation 10.2.1 tends to be used by those who traditionally work in SI units and tends more to be used by European practitioners. For the same Reynolds number and relative roughness, the ‘Imperial based friction factor’ will be exactly four times larger than the ‘SI based friction factor’.
Friction factors can be determined either from a Moody chart or, for turbulent flows, can be calculated from Equation 10.2.3, a development of the Colebrook - White formula.

However, Equation 10.2.3 is difficult to use because the friction factor appears on both sides of the equation, and it is for this reason that manual calculations are likely to be carried out by using the Moody chart.
On an SI style Moody chart, the friction factor scale might typically range from 0.002 to 0.02, whereas on an Imperial style Moody chart, this scale might range from 0.008 to 0.08.
As a general rule, for turbulent flow with Reynolds numbers between 4 000 and 100 000, ‘SI based’ friction factors will be of the order suggested by Equation 10.2.4, whilst ‘Imperial based’ friction factors will be of the order suggested by Equation 10.2.5.

The friction factor used will determine whether the D’Arcy Equation 10.2.1 or 10.2.2 is used.
For ‘SI based’ friction factors, use Equation 10.2.1; for ‘Imperial based’ friction factors, use Equation 10.2.2.
Example 10.2.1 Water pipe
Determine the velocity, friction factor and the difference in pressure between two points 1 km apart in a 150 mm constant bore horizontal pipework system if the water flowrate is 45 m³/h at 15°C.

In essence, the friction factor depends on the Reynolds number (Re) of the flowing liquid and the relative roughness (kS/d) of the inside of the pipe; the former calculated from Equation 10.2.6, and the latter from Equation 10.2.7.
Reynolds number (Re)

The pipe roughness or ‘kS’ value (often quoted as ‘curly-e - body text.jpg‘ in some texts) is taken from standard tables, and for ‘commercial steel pipe’ would generally be taken as 0.000 045 metres.
From this the relative roughness is determined (as this is what the Moody chart requires).

The friction factor can now be determined from the Moody chart and the friction head loss calculated from the relevant D’Arcy Equation.
From the European Moody chart (Figure 10.2.4),
Where: kS/D = 0.000 3 Re = 93 585: Friction factor (f) = 0.005
From the USA/AUS Moody chart (Figure 10.2.5),
Where: kS/D = 0.000 3 Re = 93 585 Friction factor (f) = 0.02
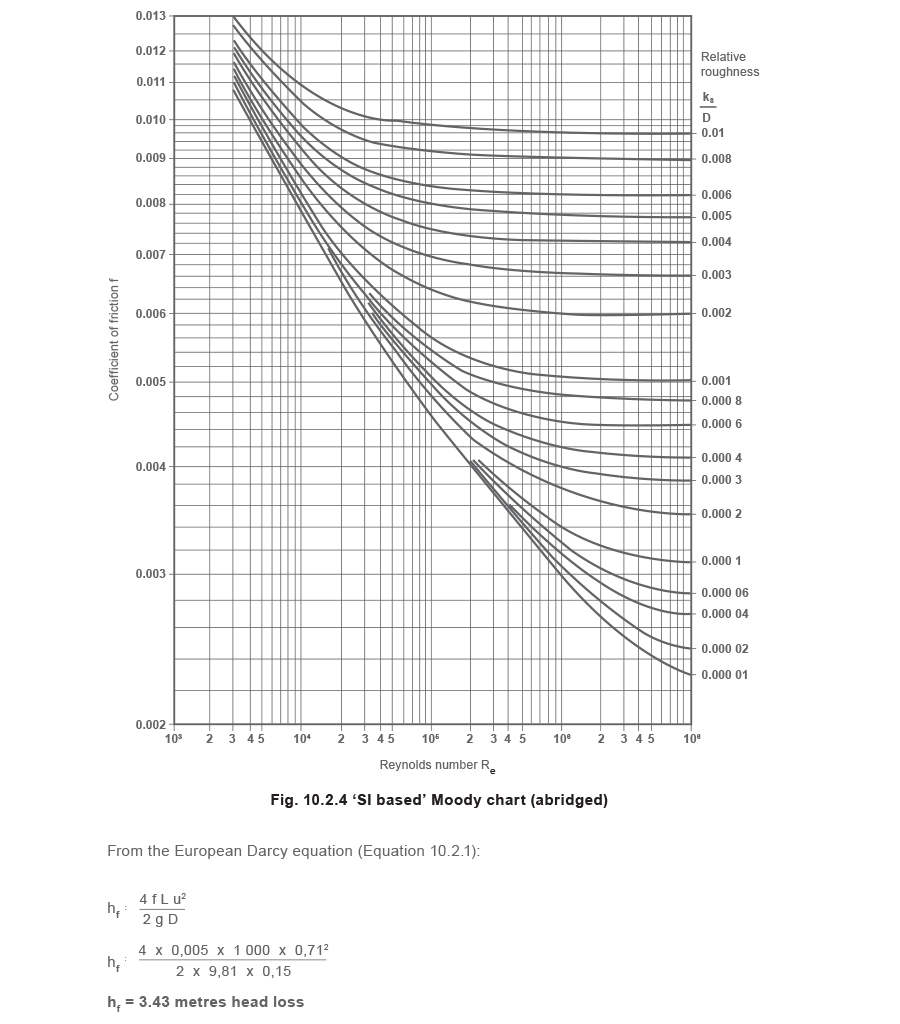
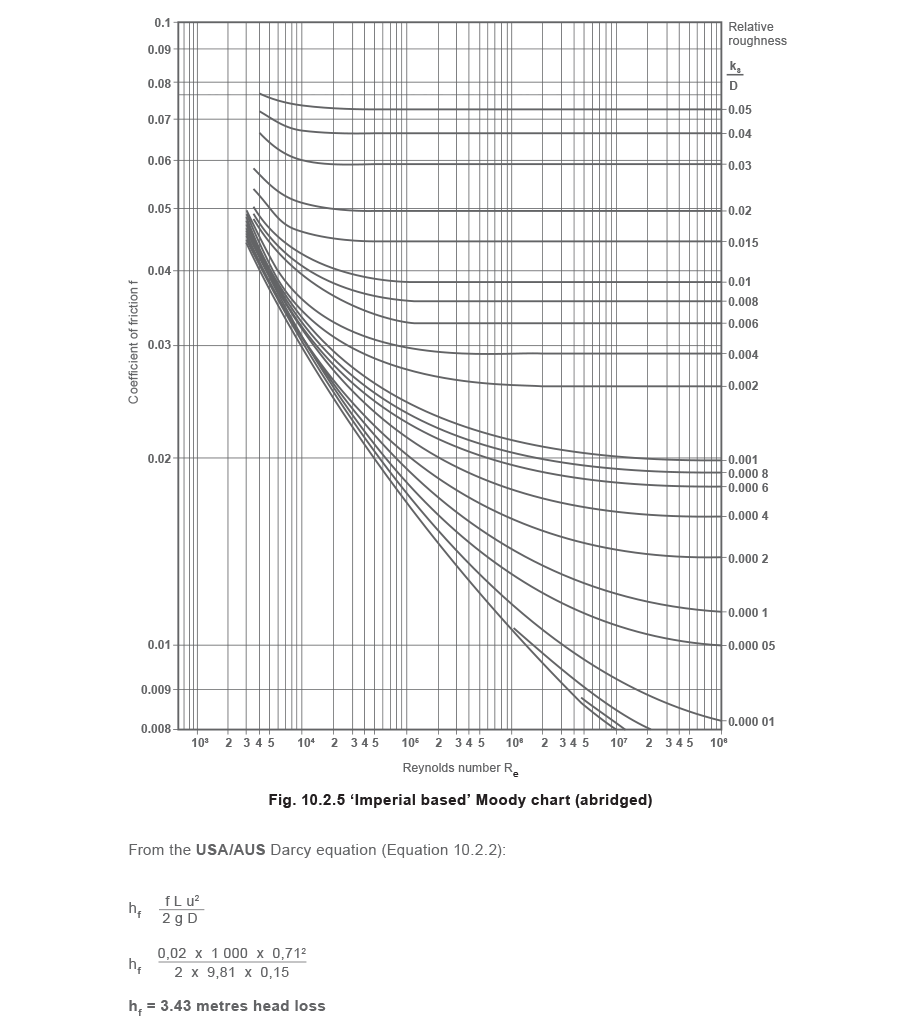
The same friction head loss is obtained by using the different friction factors and relevant D’Arcy equations.
In practice whether for water pipes or steam pipes, a balance is drawn between pipe size and pressure loss.
Pipeline sizing in steam
Oversized pipework means:
- Pipes, valves, fittings, etc. will be more expensive than necessary.
- Higher installation costs will be incurred, including support work, insulation, etc.
- For steam pipes a greater volume of condensate will be formed due to the greater heat loss. This, in turn, means that either:
- More steam trapping is required, or
- Wet steam is delivered to the point of use.
In a particular example:
- The cost of installing 80 mm steam pipework was found to be 44% higher than the cost of 50 mm pipework, which would have had adequate capacity.
- The heat lost by the insulated pipework was some 21% higher from the 80 mm pipeline than it would have been from the 50 mm pipework. Any non-insulated parts of the 80 mm pipe would lose 50% more heat than the 50 mm pipe, due to the extra heat transfer surface area.
Undersized pipework means:
- A lower pressure might be available at the point of use, which may hinder equipment performance.
- There is a risk of steam starvation due to an excessive pressure drop.
- There is a greater risk of erosion, waterhammer and noise due to the inherent increase in steam velocity.
As previously mentioned, the friction factor (f) can be difficult to determine, and the calculation itself is time consuming especially for turbulent steam flow. As a result, there are numerous graphs, tables and slide rules available for relating steam pipe sizes to flowrates and pressure drops.
One pressure drop sizing method, which has stood the test of time, is the ‘pressure factor’ method. A table of pressure factor values is used in Equation 10.2.8 to determine the pressure drop factor for a particular installation.


Example 10.2.2
Consider the system shown in Figure 10.2.6, and determine the pipe size required from the boiler to the unit heater branch line. Unit heater steam load = 270 kg/h.
Although the unit heater only requires 270 kg/h, the boiler has to supply more than this due to heat losses from the pipe.
The allowance for pipe fittings
The length of travel from the boiler to the unit heater is known, but an allowance must be included for the additional frictional resistance of the fittings. This is generally expressed in terms of ‘equivalent pipe length’. If the size of the pipe is known, the resistance of the fittings can be calculated. As the pipe size is not yet known in this example, an addition to the equivalent length can be used based on experience.
• If the pipe is less than 50 metres long, add an allowance for fittings of 10% to 20%.
• If the pipe is over 100 metres long and is a fairly straight run with few fittings, an allowance for fittings of 5% to 10% would be made.
• A similar pipe length, but with more fittings, would increase the allowance towards 20%.
In this instance, revised length = 150 m + 10% = 165 m
From Table 10.2.2 (an extract from the complete pressure factor table, Table 10.2.5, which can be found in the Appendix at the end of this Module) ‘PDF‘ can be determined by finding the pressure factors F1 and F2, and substituting them into Equation 10.2.8.
Table 10.2.2 Extract from pressure factor table (Table 10.2.5)
| Pressure bar g | Pressure factor (F) |
| 6.5 | 49.76 |
| 6.6 | 51.05 |
| 6.7 | 52.36 |
| 6.9 | 55.02 |
| 7 | 56.38 |
| 7.1 | 57.75 |
From the pressure factor table (see Table 10.2.2):
P1 = 7.0 bar g, F1 = 56.38 P2 = 6.6 bar g, F2 = 51.05
Substituting these pressure factors (P1 and P2) into Equation 10.2.8 will determine the value for PDF:

Following down the left-hand column of the pipeline capacity and pressure drop factors table (Table 10.2.6 - Extract shown in Table 10.2.3); the nearest two readings around the requirement of 0.032 are 0.030 and 0.040. The next lower factor is always selected; in this case, 0.030.
Table 10.2.3 Extract from pipeline capacity and pressure factor table (Table 10.2.6)
| Pressure drop factor (PDF) |
Pipe size (DN) |
||||||||||
| 15 | 20 | 25 | 32 | 40 | 50 | 65 | 80 | 100 | 150 | 200 | |
| Capacity (kg/h) |
|||||||||||
| 0.025 | 10.99 | 33.48 | 70.73 | 127.3 | 209.8 | 459.7 | 834.6 | 1 367 | 2 970 | 8 817 | 19 332 |
| 0.030 | 12.00 | 36.78 | 77.23 | 137.9 | 229.9 | 501.1 | 919.4 | 1 480 | 3 264 | 9 792 | 20 917 |
| 0.040 | 14.46 | 44.16 | 93.17 | 169.2 | 279.5 | 600.7 | 1 093 | 1 790 | 3 923 | 11 622 | 25 254 |
Although values can be interpolated, the table does not conform exactly to a straight-line graph, so interpolation cannot be absolutely correct. Also, it is bad practice to size any pipe up to the limit of its capacity, and it is important to have some leeway to allow for the inevitable future changes in design.
From factor 0.030, by following the row of figures to the right it will be seen that:
• A 40 mm pipe will carry 229.9 kg/h.
• A 50 mm pipe will carry 501.1 kg/h.
Since the application requires 270 kg/h, the 50 mm pipe would be selected.
Having sized the pipe using the pressure drop method, the velocity can be checked if required.

Viewed in isolation, this velocity may seem low in comparison with maximum permitted velocities. However, this steam main has been sized to limit pressure drop, and the next smaller pipe size would have given a final pressure less than the requirement of 6.6 bar g, which is unacceptable.
As can be seen, this procedure is fairly complex and can be simplified by using the nomogram shown in Figure 10.2.9 (in the Appendix of this Module). The method of use is explained in Example 10.2.3.
Example 10.2.3
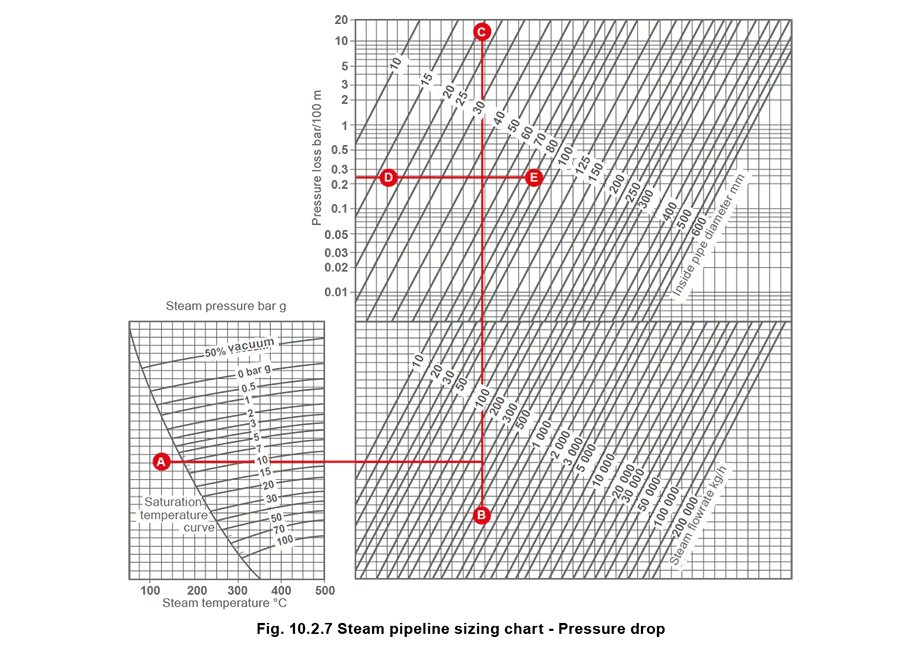
Using the data from Example 10.2.2, determine the pipe size using the nomogram shown in Figure 10.2.7.

Method:
- Select the point on the saturated steam line at 7 bar g, and mark Point A.
- From point A, draw a horizontal line to the steam flowrate of 270 kg/h, and mark Point B.
- From point B, draw a vertical line towards the top of the nomogram (Point C).
- Draw a horizontal line from 0.24 bar/100 m on the pressure loss scale (Line DE).
- The point at which lines DE and BC cross will indicate the pipe size required. In this case, a 40 mm pipe is too small, and a 50 mm pipe would be used.
It is worth noting, however, that if the pipe run is particularly long and in exposed conditions, it is worth checking the running load of the pipe covered in Module 2.12 – “Steam consumption of pipes and air heaters”. The running load should then be added on to the steam consumption to give the total steam load and the selected pipe checked to ensure it is still correctly sized.
Why is velocity important in sizing pipes?
From the knowledge gained at the beginning of this Module, and particularly the notes regarding the D’Arcy equation (Equation 10.2.1), it is acknowledged that velocity is an important factor in sizing pipes. It follows then, that if a reasonable velocity could be used for a particular fluid flowing through pipes, then velocity could be used as a practical sizing factor. As a general rule, a velocity of 25 to 40 m/s is used when saturated steam is the medium.
40 m/s should be considered a practical limit, as above this, noise and erosion will take place particularly if the steam is wet. Some National standards quote velocities up to 76 m/s for saturated steam. This can only be feasible if; the steam is dry, the pipe is very well insulated, relatively short, straight, horizontal and can supply the required pressure at the point of use.
Even these velocities can be high in terms of their effect on pressure drop. In longer supply lines, it is often necessary to restrict velocities to 15 m/s to avoid high pressure drops. It is recommended that pipelines over 50 m long are always checked for pressure drop, no matter what the velocity.
By using Table 10.2.4 as a guide, it is possible to select pipe sizes from known data; steam pressure, velocity and flowrate.
Table 10.2.4 Saturated steam pipeline capacities in kg/h for different velocities (Schedule 40 pipe)
| Pressure bar g |
Velocity m/s |
Pipe size (nominal) |
||||||||||
| 15 | 20 | 25 | 32 | 40 | 50 | 65 | 80 | 100 | 125 | 150 | ||
| Actual inside pipe diameter Schedule 40 |
||||||||||||
| 15.8 | 20.93 | 26.64 | 35.04 | 40.9 | 52.5 | 62.7 | 77.92 | 102.26 | 128.2 | 154.05 | ||
| Pipeline capacity kg/h |
||||||||||||
| 0.4 |
15 | 9 | 15 | 25 | 43 | 58 | 95 | 136 | 210 | 362 | 569 | 822 |
| 25 | 14 | 25 | 41 | 71 | 97 | 159 | 227 | 350 | 603 | 948 | 1 369 | |
| 40 | 23 | 40 | 66 | 113 | 154 | 254 | 363 | 561 | 965 | 1 517 | 2 191 | |
| 0.7 |
15 | 10 | 18 | 29 | 51 | 69 | 114 | 163 | 251 | 433 | 681 | 983 |
| 25 | 17 | 30 | 49 | 85 | 115 | 190 | 271 | 419 | 722 | 1 135 | 1 638 | |
| 40 | 28 | 48 | 78 | 136 | 185 | 304 | 434 | 671 | 1 155 | 1 815 | 2 621 | |
| 1 |
15 | 12 | 21 | 34 | 59 | 81 | 133 | 189 | 292 | 503 | 791 | 1 142 |
| 25 | 20 | 35 | 57 | 99 | 134 | 221 | 315 | 487 | 839 | 1 319 | 1 904 | |
| 40 | 32 | 56 | 91 | 158 | 215 | 354 | 505 | 779 | 1342 | 2 110 | 3 046 | |
| 2 |
15 | 18 | 31 | 50 | 86 | 118 | 194 | 277 | 427 | 735 | 1 156 | 1 669 |
| 25 | 29 | 51 | 83 | 144 | 196 | 323 | 461 | 712 | 1 226 | 1 927 | 2 782 | |
| 40 | 47 | 82 | 133 | 230 | 314 | 517 | 737 | 1 139 | 1 961 | 3 083 | 4 451 | |
| 3 |
15 | 23 | 40 | 65 | 113 | 154 | 254 | 362 | 559 | 962 | 1 512 | 2 183 |
| 25 | 38 | 67 | 109 | 188 | 256 | 423 | 603 | 931 | 1 603 | 2 520 | 3 639 | |
| 40 | 61 | 107 | 174 | 301 | 410 | 676 | 964 | 1 490 | 2 565 | 4 032 | 5 822 | |
| 4 |
15 | 28 | 50 | 80 | 139 | 190 | 313 | 446 | 689 | 1 186 | 1 864 | 2 691 |
| 25 | 47 | 83 | 134 | 232 | 316 | 521 | 743 | 1 148 | 1 976 | 3 106 | 4 485 | |
| 40 | 75 | 132 | 215 | 371 | 506 | 833 | 1 189 | 1 836 | 3 162 | 4 970 | 7 176 | |
| 5 |
15 | 34 | 59 | 96 | 165 | 225 | 371 | 529 | 817 | 1 408 | 2 213 | 3 195 |
| 25 | 56 | 98 | 159 | 276 | 375 | 619 | 882 | 1 362 | 2 347 | 3 688 | 5 325 | |
| 40 | 90 | 157 | 255 | 441 | 601 | 990 | 1 411 | 2 180 | 3 755 | 5 901 | 8 521 | |
| 6 |
15 | 39 | 68 | 111 | 191 | 261 | 430 | 613 | 947 | 1 631 | 2 563 | 3 700 |
| 25 | 65 | 114 | 184 | 319 | 435 | 716 | 1 022 | 1 578 | 2 718 | 4 271 | 6 167 | |
| 40 | 104 | 182 | 295 | 511 | 696 | 1 146 | 1 635 | 2 525 | 4 348 | 6 834 | 9 867 | |
| 7 |
15 | 44 | 77 | 125 | 217 | 296 | 487 | 695 | 1 073 | 1 848 | 2 904 | 4 194 |
| 25 | 74 | 129 | 209 | 362 | 493 | 812 | 1 158 | 1 788 | 3 080 | 4 841 | 6 989 | |
| 40 | 118 | 206 | 334 | 579 | 788 | 1 299 | 1 853 | 2 861 | 4 928 | 7 745 | 11 183 | |
| 8 |
15 | 49 | 86 | 140 | 242 | 330 | 544 | 775 | 1 198 | 2 063 | 3 242 | 4 681 |
| 25 | 82 | 144 | 233 | 404 | 550 | 906 | 1 292 | 1 996 | 3 438 | 5 403 | 7 802 | |
| 40 | 131 | 230 | 373 | 646 | 880 | 1 450 | 2 068 | 3 194 | 5 501 | 8 645 | 12 484 | |
| 10 |
15 | 60 | 105 | 170 | 294 | 401 | 660 | 942 | 1 455 | 2 506 | 3 938 | 5 686 |
| 25 | 100 | 175 | 283 | 490 | 668 | 1 101 | 1 570 | 2 425 | 4 176 | 6 563 | 9 477 | |
| 40 | 160 | 280 | 453 | 785 | 1 069 | 1 761 | 2 512 | 3 880 | 6 682 | 10 502 | 15 164 | |
| 14 |
15 | 80 | 141 | 228 | 394 | 537 | 886 | 1 263 | 1 951 | 3 360 | 5 281 | 7 625 |
| 25 | 134 | 235 | 380 | 657 | 896 | 1 476 | 2 105 | 3 251 | 5 600 | 8 801 | 12 708 | |
| 40 | 214 | 375 | 608 | 1 052 | 1 433 | 2 362 | 3 368 | 5 202 | 8 960 | 14 082 | 20 333 | |
Alternatively the pipe size can be calculated arithmetically. The following information is required, and the procedure used for the calculation is outlined below.
Information required to calculate the required pipe size:

Example 10.2.4
A process requires 5 000 kg/h of dry saturated steam at 7 bar g. For the flow velocity not to exceed 25 m/s, determine the pipe size.

Since the steam velocity must not exceed 25 m/s, the pipe size must be at least 130 mm; the nearest commercially available size, 150 mm, would be selected.
Again, a nomogram has been created to simplify this process, see Figure 10.2.8.
Example 10.2.5
Using the information from Example 10.2.4, use Figure 10.2.8 to determine the minimum acceptable pipe size
Inlet pressure = 7 bar g
Steam flowrate = 5 000 kg/h
Maximum velocity = 25 m/s
Method:
- Draw a horizontal line from the saturation temperature line at 7 bar g (Point A) on the pressure scale to the steam mass flowrate of 5 000 kg/h (Point B).
- From point B, draw a vertical line to the steam velocity of 25 m/s (Point C). From point C, draw a horizontal line across the pipe diameter scale (Point D).
- A pipe with a bore of 130 mm is required; the nearest commercially available size, 150 mm, would be selected.

Sizing pipes for superheated steam duty
Superheated steam can be considered as a dry gas and therefore carries no moisture. Consequently there is no chance of pipe erosion due to suspended water droplets, and steam velocities can be as high as 50 to 70 m/s if the pressure drop permits this. The nomograms in Figures 10.2.9 and 10.2.10 can also be used for superheated steam applications.
Example 10.2.6
Utilising the waste heat from a process, a boiler/superheater generates 30 t/h of superheated steam at 50 bar g and 450°C for export to a neighbouring power station. If the velocity is not to exceed 50 m/s, determine:
1. The pipe size based on velocity (use Figure 10.2.10).
2. The pressure drop if the pipe length, including allowances, is 200 m (use Figure 10.2.9).
Part 1
- Using Figure 10.2.8, draw a vertical line from 450°C on the temperature axis until it intersects the 50 bar line (Point A).
- From point A, project a horizontal line to the left until it intersects the steam ‘mass flowrate’ scale of 30 000 kg/h (30 t/h) (Point B).
- From point B, project a line vertically upwards until it intersects 50 m/s on the ‘steam velocity’ scale (Point C).
- From Point C, project a horizontal line to the right until it intersects the ‘inside pipe diameter’ scale.
The ‘inside pipe diameter’ scale recommends a pipe with an inside diameter of about 120 mm. From Table 10.2.1 and assuming that the pipe will be Schedule 80 pipe, the nearest size would be 150 mm, which has a bore of 146.4 mm.
Part 2
- Using Figure 10.2.7, draw a vertical line from 450°C on the temperature axis until it intersects the 50 bar line (Point A).
- From point A, project a horizontal line to the right until it intersects the ‘steam mass flowrate’ scale of 30 000 kg/h (30 t/h) (Point B).
- From point B, project a line vertically upwards until it intersects the ‘inside pipe diameter’ scale of (approximately) 146 mm (Point C).
- From Point C, project a horizontal line to the left until it intersects the ‘pressure loss bar/100 m’ scale (Point D).
The ‘pressure loss bar/100 m’ scale reads about 0.9 bar/100 m. The pipe length in the example is 200 m, so the pressure drop is:

This pressure drop must be acceptable at the process plant.
Using formulae to establish steam flowrate on pressure drop
Empirical formulae exist for those who prefer to use them. Equations 10.2.9 and 10.2.10 are shown below. These have been tried and tested over many years, and which appear to give results close to the pressure factor method. The advantage of using these formulae is that they can be programmed into a scientific calculator, or a spreadsheet, and consequently used without the need to look up tables and charts. Equation 10.2.10 requires the specific volume of steam to be known, which means it is necessary to look up this value from a steam table. Also, Equation 10.2.10 should be restricted to a maximum pipe length of 200 metres.
Equation 10.2.9 Pressure drop formula 1
Equation 10.2.10 Pressure drop forumla 2 (Maximum pipe length: 200 metres)


Summery
- The selection of piping material and the wall thickness required for a particular installation is stipulated in standards such as EN 45510 and ASME 31.1.
- Selecting the appropriate pipe size (nominal bore) for a particular application is based on accurately identifying pressure and flowrate. The pipe size may be selected on the basis of:
- Velocity (usually pipes less than 50 m in length).
- Pressure drop (as a general rule, the pressure drop should not normally exceed 0.1 bar/50 m.
Appendix
Table 10.2.5 Pressure drop factor (F) table
| Pressure bar abs | Pressure factor (F) | Pressure bar g | Pressure factor (F) | Pressure bar g | Pressure factor (F) | Pressure bar g | Pressure factor (F) | |||
| 0.05 | 0.0301 | 1.3 | 5.076 | 4.5 | 27.32 | 9.4 | 93.66 | |||
| 0.1 | 0.0115 | 1.35 | 5.291 | 4.6 | 28.28 | 9.5 | 95.41 | |||
| 0.15 | 0.0253 | 1.4 | 5.51 | 4.7 | 29.27 | 9.6 | 97.18 | |||
| 0.2 | 0.0442 | 1.45 | 5.734 | 4.8 | 30.27 | 9.7 | 98.96 | |||
| 0.25 | 0.0681 | 1.5 | 5.961 | 4.9 | 31.29 | 9.8 | 100.75 | |||
| 0.3 | 0.097 | 1.55 | 6.193 | 5 | 32.32 | 9.9 | 102.57 | |||
| 0.35 | 0.1308 | 1.6 | 6.429 | 5.1 | 33.37 | 10 | 104.4 | |||
| 0.4 | 0.1694 | 1.65 | 6.67 | 5.2 | 34.44 | 10.2 | 108.1 | |||
| 0.45 | 0.2128 | 1.7 | 6.915 | 5.3 | 35.52 | 10.4 | 111.87 | |||
| 0.5 | 0.261 | 1.75 | 7.164 | 5.4 | 36.62 | 10.6 | 115.7 | |||
| 0.55 | 0.314 | 1.8 | 7.417 | 5.5 | 37.73 | 10.8 | 119.59 | |||
| 0.6 | 0.3716 | 1.85 | 7.675 | 5.6 | 38.86 | 11 | 123.54 | |||
| 0.65 | 0.434 | 1.9 | 7.937 | 5.7 | 40.01 | 11.2 | 127.56 | |||
| 0.7 | 0.501 | 1.95 | 8.203 | 5.8 | 41.17 | 11.4 | 131.64 | |||
| 0.75 | 0.5727 | 2 | 8.473 | 5.9 | 42.35 | 11.6 | 135.78 | |||
| 0.8 | 0.6489 | 2.05 | 8.748 | 6 | 43.54 | 11.8 | 139.98 | |||
| 0.85 | 0.7298 | 2.1 | 9.026 | 6.1 | 44.76 | 12 | 144.25 | |||
| 0.9 | 0.8153 | 2.15 | 9.309 | 6.2 | 45.98 | 12.2 | 148.57 | |||
| 0.95 | 0.9053 | 2.2 | 9.597 | 6.3 | 47.23 | 12.4 | 152.96 | |||
| 1.013 | 1.025 | 2.25 | 9.888 | 6.4 | 48.48 | 12.6 | 157.41 | |||
| 2.3 | 10.18 | 6.5 | 49.76 | 12.8 | 161.92 | |||||
| Pressure bar g | Pressure factor (F) | 2.35 | 10.48 | 6.6 | 51.05 | 13 | 166.5 | |||
| 2.4 | 10.79 | 6.7 | 52.36 | 13.2 | 171.13 | |||||
| 0 | 1.025 | 2.45 | 11.4 | 6.8 | 53.68 | 13.4 | 175.83 | |||
| 0.05 | 1.126 | 2.5 | 11.41 | 6.9 | 55.02 | 13.6 | 180.58 | |||
| 0.1 | 1.23 | 2.55 | 11.72 | 7 | 56.38 | 13.8 | 185.4 | |||
| 0.15 | 1.339 | 2.6 | 12.05 | 7.1 | 57.75 | 14 | 190.29 | |||
| 0.2 | 1.453 | 2.65 | 12.37 | 7.2 | 59.13 | 14.2 | 195.23 | |||
| 0.25 | 1.572 | 2.7 | 12.7 | 7.3 | 60.54 | 14.4 | 200.23 | |||
| 0.3 | 1.694 | 2.75 | 13.03 | 7.4 | 61.96 | 14.6 | 205.3 | |||
| 0.35 | 1.822 | 2.8 | 13.37 | 7.5 | 63.39 | 14.8 | 210.42 | |||
| 0.4 | 1.953 | 2.85 | 13.71 | 7.6 | 64.84 | 15 | 215.61 | |||
| 0.45 | 2.09 | 2.9 | 14.06 | 7.7 | 66.31 | 15.2 | 220.86 | |||
| 0.5 | 2.23 | 2.95 | 14.41 | 7.8 | 67.79 | 15.4 | 226.17 | |||
| 0.55 | 2.375 | 3 | 14.76 | 7.9 | 69.29 | 15.6 | 231.5 | |||
| 0.6 | 2.525 | 3.1 | 15.48 | 8 | 70.8 | 15.8 | 236.97 | |||
| 0.65 | 2.679 | 3.2 | 16.22 | 8.1 | 72.33 | 16 | 242.46 | |||
| 0.7 | 2.837 | 3.3 | 16.98 | 8.2 | 73.88 | 16.2 | 248.01 | |||
| 0.75 | 2.999 | 3.4 | 17.75 | 8.3 | 75.44 | 16.4 | 253.62 | |||
| 0.8 | 3.166 | 3.5 | 18.54 | 8.4 | 77.02 | 16.6 | 259.3 | |||
| 0.85 | 3.338 | 3.6 | 19.34 | 8.5 | 78.61 | 16.8 | 265.03 | |||
| 0.9 | 3.514 | 3.7 | 20.16 | 8.6 | 80.22 | 17 | 270.83 | |||
| 0.95 | 3.694 | 3.8 | 21 | 8.7 | 81.84 | 17.2 | 276.69 | |||
| 1 | 3.878 | 3.9 | 21.85 | 8.8 | 83.49 | 17.4 | 282.6 | |||
| 1.05 | 4.067 | 4 | 22.72 | 8.9 | 85.14 | 17.6 | 288.58 | |||
| 1.1 | 4.26 | 4.1 | 23.61 | 9 | 86.81 | 17.8 | 294.52 | |||
| 1.15 | 4.458 | 4.2 | 24.51 | 9.1 | 88.5 | 18 | 300.72 | |||
| 1.2 | 4.66 | 4.3 | 25.43 | 9.2 | 90.2 | |||||
| 1.25 | 4.866 | 4.4 | 26.36 | 9.3 | 91.92 |
Table 10.2.6 Pipeline capacity from pressure drop factor
| Pressure drop factor (PDF) | Pipe size (mm) |
||||||||||||
| 15 | 20 | 25 | 32 | 40 | 50 | 65 | 80 | 100 | 150 | 200 | 250 | 300 | |
| Capacity (kg/h) | |||||||||||||
| 0.00016 | 30.40 | 55.41 | 90.72 | 199.1 | 598.2 | 1 275 | 2 329 | 3 800 | |||||
| 0.00020 | 16.18 | 34.32 | 62.77 | 103.0 | 225.6 | 662.0 | 1 437 | 2 623 | 4 276 | ||||
| 0.00025 | 10.84 | 17.92 | 38.19 | 69.31 | 113.2 | 249.9 | 735.5 | 1 678 | 2 904 | 4 715 | |||
| 0.00030 | 11.95 | 19.31 | 41.83 | 75.85 | 124.1 | 271.2 | 804.5 | 1 733 | 3 172 | 5 149 | |||
| 0.00035 | 6.86 | 12.44 | 20.59 | 43.76 | 80.24 | 130.0 | 285.3 | 845.3 | 1 823 | 3 346 | 5 530 | ||
| 0.00045 | 3.62 | 7.94 | 14.56 | 23.39 | 50.75 | 92.68 | 150.9 | 333.2 | 979.7 | 2 118 | 3 884 | 6 267 | |
| 0.00055 | 4.04 | 8.99 | 16.18 | 26.52 | 57.09 | 103.8 | 170.8 | 373.1 | 1 101 | 2 382 | 4 338 | 7 057 | |
| 0.00065 | 4.46 | 9.56 | 17.76 | 29.14 | 62.38 | 113.8 | 186.7 | 409.8 | 1 207 | 2 595 | 4 781 | 7 741 | |
| 0.00075 | 4.87 | 10.57 | 19.31 | 31.72 | 68.04 | 124.1 | 203.2 | 445.9 | 1 315 | 2 836 | 5 172 | 8 367 | |
| 0.00085 | 5.52 | 11.98 | 21.88 | 35.95 | 77.11 | 140.7 | 230.2 | 505.4 | 1 490 | 3 215 | 5 861 | 9 482 | |
| 0.00100 | 1.96 | 5.84 | 12.75 | 23.50 | 38.25 | 81.89 | 148.6 | 245.2 | 539.4 | 1 579 | 3 383 | 6 228 | 10 052 |
| 0.00125 | 2.10 | 6.26 | 13.57 | 24.96 | 40.72 | 87.57 | 159.8 | 261.8 | 577.9 | 1 699 | 3 634 | 6 655 | 10 639 |
| 0.00150 | 2.39 | 7.35 | 15.17 | 28.04 | 45.97 | 98.84 | 179.3 | 295.1 | 652.8 | 1 908 | 4 091 | 7 493 | 11 999 |
| 0.00175 | 2.48 | 7.51 | 16.30 | 29.61 | 49.34 | 103.4 | 188.8 | 311.1 | 686.5 | 2 017 | 4 291 | 7 852 | 13 087 |
| 0.0020 | 2.84 | 8.58 | 18.63 | 33.83 | 56.39 | 118.2 | 215.8 | 355.5 | 784.6 | 2 305 | 4 904 | 8 974 | 14 956 |
| 0.0025 | 3.16 | 9.48 | 20.75 | 37.25 | 61.30 | 132.0 | 240.5 | 391.3 | 881.7 | 2 456 | 5 422 | 10 090 | 16 503 |
| 0.0030 | 3.44 | 10.34 | 22.50 | 40.45 | 66.66 | 143.4 | 262.0 | 429.8 | 924.4 | 2 767 | 6 068 | 11 033 | 18 021 |
| 0.0040 | 4.17 | 12.50 | 26.97 | 48.55 | 80.91 | 173.1 | 313.8 | 514.9 | 1 128 | 3 330 | 7 208 | 13 240 | 21 625 |
| 0.0050 | 4.71 | 14.12 | 30.40 | 54.92 | 90.23 | 196.1 | 354.0 | 578.6 | 1 275 | 3 727 | 8 189 | 14 858 | 24 469 |
| 0.0060 | 5.25 | 15.69 | 35.80 | 60.31 | 99.05 | 215.8 | 392.3 | 647.3 | 1 412 | 4 148 | 9 072 | 16 476 | 26 970 |
| 0.0080 | 6.08 | 18.34 | 39.23 | 70.12 | 116.2 | 251.5 | 456.0 | 750.3 | 1 648 | 4 879 | 10 543 | 19 173 | 31 384 |
| 0.0100 | 6.86 | 20.64 | 44.13 | 79.44 | 130.4 | 283.9 | 514.9 | 845.9 | 1 863 | 5 492 | 11 867 | 21 576 | 35 307 |
| 0.0125 | 7.35 | 22.20 | 47.28 | 81.00 | 140.1 | 302.1 | 547.3 | 901.9 | 1 983 | 5 867 | 12 697 | 23 074 | 37 785 |
| 0.0150 | 8.27 | 25.00 | 53.33 | 95.62 | 157.2 | 342.0 | 620.6 | 1 020 | 2 230 | 6 620 | 14 251 | 25 974 | 42 616 |
| 0.0175 | 8.58 | 26.39 | 55.78 | 100.4 | 165.6 | 360.4 | 665.1 | 1 073 | 2 360 | 6 994 | 15 017 | 27 461 | 44 194 |
| 0.0200 | 9.80 | 30.16 | 63.75 | 114.7 | 189.3 | 411.9 | 760.1 | 1 226 | 2 697 | 7 993 | 17 163 | 31 384 | 50 508 |
| 0.0250 | 10.99 | 33.48 | 70.73 | 127.3 | 209.8 | 459.7 | 834.6 | 1 367 | 2 970 | 8 817 | 19 332 | 34 750 | 56 581 |
| 0.0300 | 12.00 | 36.78 | 77.23 | 137.9 | 229.9 | 501.1 | 919.4 | 1 480 | 3 264 | 9 792 | 20 917 | 37 697 | 62 522 |
| 0.0400 | 14.46 | 44.16 | 93.17 | 169.2 | 279.5 | 600.7 | 1 093 | 1 790 | 3 923 | 11 622 | 25 254 | 45 604 | 75 026 |
| 0.0500 | 16.43 | 49.53 | 104.4 | 191.2 | 313.8 | 676.7 | 1 231 | 2 020 | 4 413 | 13 044 | 28 441 | 51 489 | 85 324 |
| 0.060 | 18.14 | 52.96 | 115.7 | 210.8 | 343.2 | 750.3 | 1 373 | 2 231 | 4 855 | 14 368 | 31 384 | 57 373 | |
| 0.080 | 21.08 | 62.28 | 134.8 | 245.2 | 402.1 | 872.8 | 1 594 | 2 599 | 5 688 | 16 672 | 36 532 | ||
| 0.100 | 24.03 | 70.12 | 152.0 | 277.0 | 456.0 | 980.7 | 1 804 | 2 942 | 6 424 | 18 879 | |||
| 0.120 | 25.99 | 77.48 | 167.7 | 306.5 | 500.2 | 1 079 | 1 986 | 3 236 | 7 110 | 20 841 | |||
| 0.150 | 28.50 | 84.13 | 183.9 | 334.2 | 551.7 | 1 195 | 2 161 | 3 494 | 7 769 | ||||
| 0.200 | 34.32 | 102.0 | 220.7 | 402.1 | 622.0 | 1 427 | 2 599 | 4 217 | 9 317 | ||||
| 0.250 | 37.72 | 112.7 | 245.2 | 447.9 | 735.5 | 1 565 | 2 876 | 4 668 | |||||
| 0.300 | 41.37 | 122.7 | 266.6 | 487.3 | 804.5 | 1 710 | 3 126 | 5 057 | |||||
| 0.350 | 43.34 | 128.7 | 283.2 | 514.9 | 841.0 | 1 802 | 3 261 | ||||||
| 0.400 | 49.93 | 147.1 | 323.6 | 588.4 | 961.1 | 2 059 | 3 727 | ||||||
| 0.450 | 50.31 | 150.0 | 326.6 | 600.2 | 979.9 | 2 083 | |||||||
| 0.500 | 55.90 | 166.7 | 362.9 | 666.9 | 1 089 | 2 314 | |||||||
| 0.600 | 62.28 | 185.3 | 402.1 | 735.5 | 1 201 | ||||||||
| 0.700 | 63.07 | 188.8 | 407.6 | 750.9 | |||||||||
| 0.800 | 72.08 | 215.8 | 465.8 | 858.1 | |||||||||
| 0.900 | 73.28 | 218.4 | 476.6 | ||||||||||